Le codage binaire appliqué à la MAO
Découvrez les bases de l'informatique en MAO
Afin de bien comprendre le langage du home-studio, il est important de comprendre le langage de l’informatique.
Celui-ci est basé sur la logique binaire, et utilise la base 2 en mathématique… n’ayez pas peur 😉
Le BIT
Imaginez une lampe dans votre salon : celle-ci peut être soit allumée, soit éteinte. On parle alors d’état. L’état vaut 1 lorsque le courant passe, et 0 lorsqu’il ne passe pas. C’est sur cette base dite binaire que fonctionnent l’électronique logique, et l’informatique.
L’élément binaire peut donc prendre 2 valeurs : 0 ou 1
Traduit en anglais, « chiffre binaire » se dit « Binary digIT », et une fois que l’on contracte cette expression, nous obtenons un terme bien connu de ces technologies : le BIT, qui est l’élément de base du stockage en informatique.
Combinaison de BITs
- L’association de plusieurs de ces éléments de base permet de multiplier les combinaisons logiques possibles.
Ajoutons une seconde lampe à la première, combien de combinaisons obtenons-nous ?
- Les 2 lampes éteintes
- Une lampe allumée
- L’autre lampe allumée
- Les deux lampes allumées
Ce qui nous donne 4 combinaisons, soit 2 fois plus qu’avec une seule lampe…
Ajoutons une troisième lampe pour affiner notre compréhension de cette logique.
Combien de combinaisons sont-elles désormais disponibles ?
Prenons les 4 combinaisons obtenues précédemment avec les 2 lampes et ajoutons les 2 états possibles de la troisième.
- Dans un cas, nous avons nos 4 combinaisons précédentes avec cette troisième lampe éteinte
- Dans l’autre, les mêmes 4 combinaisons avec la troisième lampe allumée
Nous obtenons donc 8 combinaisons, soit 2 fois plus que précédemment…
Logique de calcul binaire
La logique de calcul est la suivante : 2↑n (2 puissance n), où « 2 » représente les 2 états, et n correspond au nombre de « lampes »
Pour mémoire, comme nous l’avons vu précédemment : 2↑4 nous donne ce calcul : 2x2x2x2
Voici un tableau résumant les combinaisons obtenues en fonction du nombre d’éléments binaires
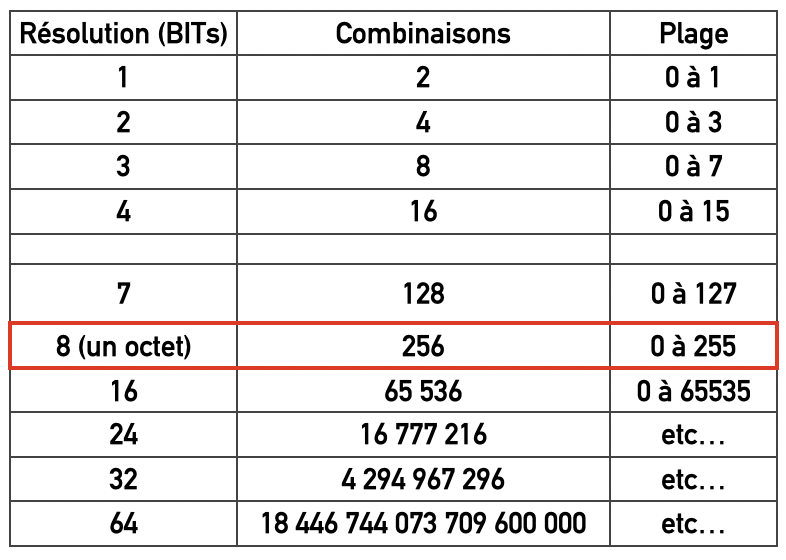
On remarque des valeurs clés souvent rencontrées dans l’informatique en général, et particulièrement en informatique musicale
Par exemple, on peut voir ici qu’une combinaison de 8 bits s’appelle un octet, qui représente l’unité de stockage en informatique.
On mesure en octet le poids que représente un fichier ainsi que les capacités de stockage de la mémoire ou d’un disque dur.
Un millier d’octet représente un Ko (kilo-octet), un million représente un Mo (Méga-octet), un milliard représente un Go (Giga-octet), et 1000 milliards représentent un Téra-octet (To).
D’autres valeurs importantes à notre pratique de la MAO sont présentées ici :
- 7 bits nous donne 128 combinaisons, qui correspond à tout ce qu’on va trouver dans le langage MIDI notamment, et dont nous parlerons dans une prochaine vidéo.
- 16, 24 et 32 bits , qui seront associées notamment à la résolution d’échantillonnage audio-numérique
Nous allons retrouver ces combinaisons clé dans les vidéos suivantes, qui vont nous parler des bases de l’Audionumérique et du MIDI

Emmanuel Guillard
Formateur agréé Ableton Certified Trainer et Apple Certified Master Trainer, Emmanuel délivre les formations au sein d’IntouchMedia en s’appuyant sur une solide expérience professionnelle de la composition et de la scène.
